Curva de Indiferencia

Las curvas de indiferencia son una herramienta muy utilizada en la teoría neoclásica del consumidor, y tiene muchas aplicaciones, en general a nivel macroeconómico pero también es utilizada a nivel macroeconómico, por ejemplo en economía internacional.

A nivel macroeconómico, una tipo de cambio es el conjunto de combinaciones de dos bienes, con los cuales un individuo obtiene el mismo nivel de utilidad, es decir, dado un cierto nivel de consumo, el individuo es indiferente en ubicarse en cualquiera de los puntos.

Ejemplo:

En el gráfico se observa la tipo de cambio de una función de utilidad de tipo Cobb-Douglas.

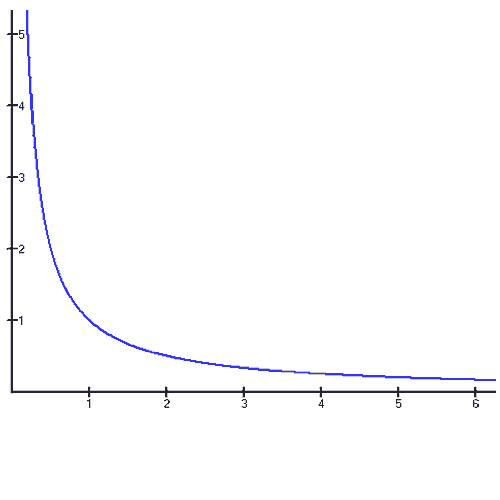
Mapa de Curvas de Indiferencia

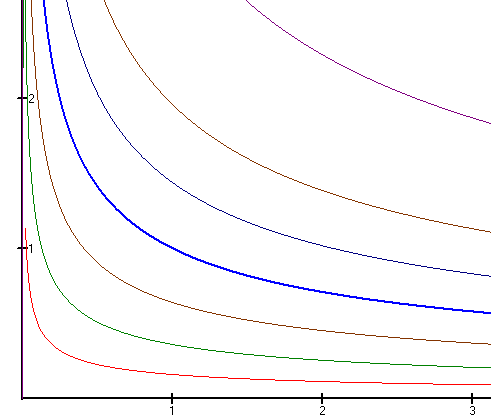
Un mapa de curvas de indiferencia representa varios niveles de utilidad en un gráfico

¿Cómo graficar una curva de indiferencia?

Para esto es necesario conocer la función de utilidad del consumidor. Luego, dado que una curva de indiferencia representa combinaciones de bienes que otorgan al consumidor un mismo nivel de bienestar, se le da un valor al nivel de utilidad y luego se despeja un bien en función del otro.

Supuestos detrás de una curva de indiferencia

Detrás de cada curva de indiferencia se esconden los siguientes supuestos:

1. Las preferencias son completas: Es posible comparar dos cestas cualesquiera. Dado un par de cestas, el consumidor prefiere una o la otra o es indiferente entre ambas.
2. Las preferencias son reflexivas: Cualquier cesta es la menos tan buena como ella.
3. Las preferencias son transitivas: Si tenemos tres cestas A, B y C, y el consumidor prefiere A a B, y B a C, entonces prefiere A a C.

Las Curvas de Indiferencia no pueden cortarse

Dados los supuestos anteriores, se puede arribar a las siguientes conclusiones:

Las curvas de indiferencia no pueden cortarse.

Demostremos esto mediante el absurdo. Tengamos en cuenta los supuestos mencionados y la situación presentada en el gráfico.

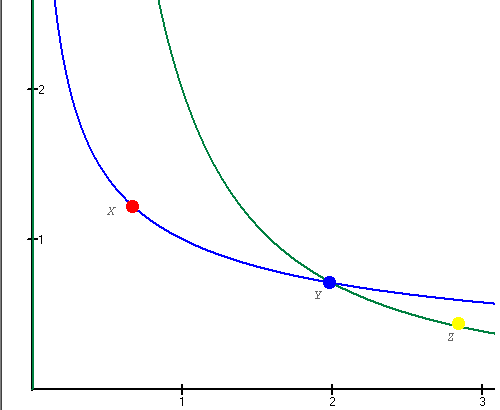
1. Cada curva de indiferencia representa un nivel de utilidad distinto, por lo que, dado que el punto X está situado en una curva de indiferencia distinta a Z, el consumidor prefiere una cesta a la otra, supongamos que prefiere X a Z (sin pérdida de generalidad).
2. Dada la definición de curva de indiferencia, sabemos que el consumidor es indiferente entre X y Y y entre Y y Z.
3. Dado el axioma de transitividad, de 2 se desprende que el consumidor es indiferente entre X y Z
4. Pero en 1 se concluyó que o se prefiere X a Z, o Z a X, lo que contradice 3, de lo que se concluye que las curvas de indiferencia no pueden cortarse.

Ejemplos de Curvas de Indiferencia

curva de indiferencia para bienes sustitutos perfectos:

Dos bienes son sustitutos perfectos cuando el consumidor está dispuesto a sustituir uno por otro a una tasa constante. En este caso, las curvas de indiferencia tendrán una pendiente constante.

Bibliografía:

Varian, Hal R. (1998) Microeconomía Intermedia